Note: I originally wrote this article in 2008 and published it on my Sworded Contemplations blog. There it has languished over the years gaining the occasional comment, reference, etc. In an effort to consolidate some of my work in one place, I have chosen to move it over to this forum.
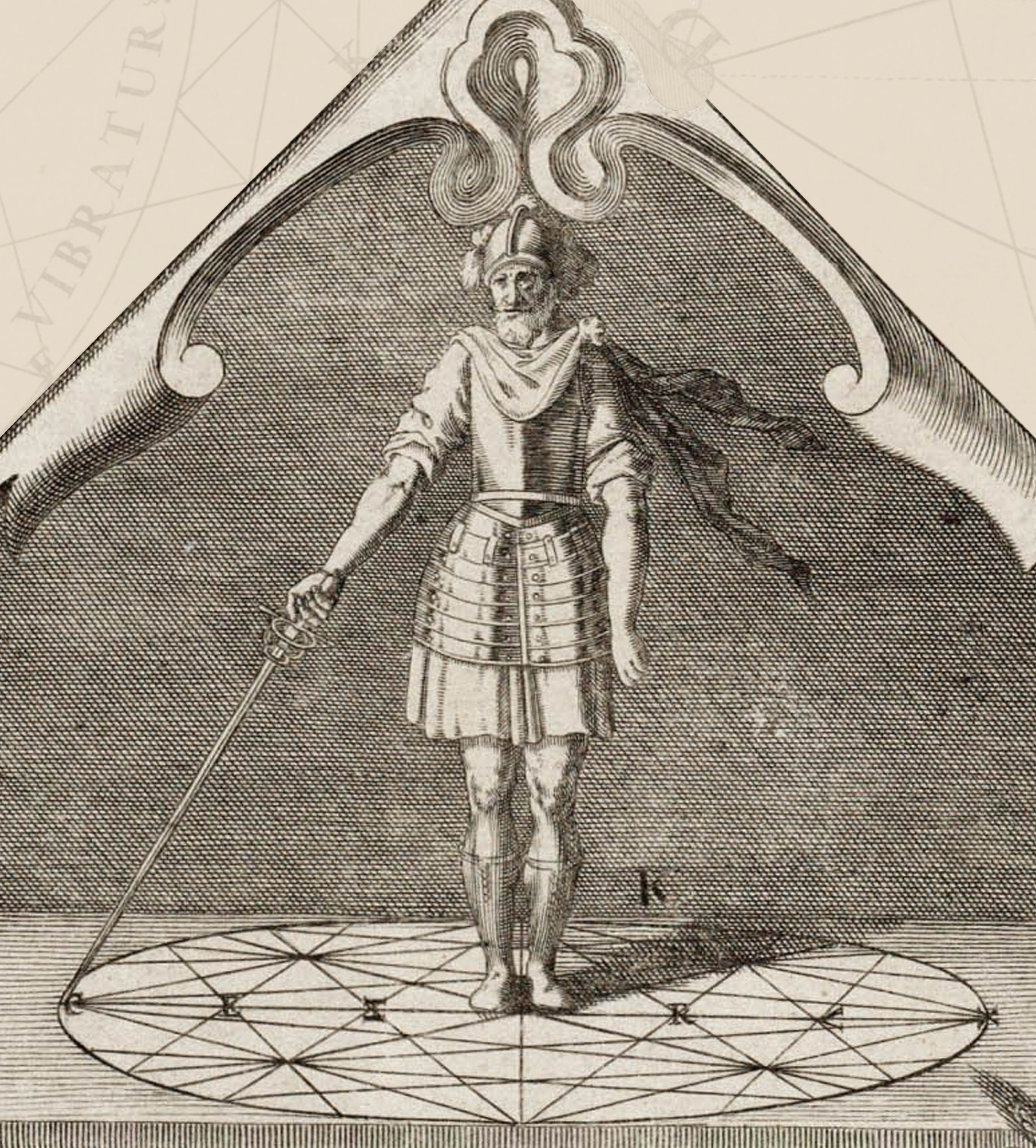
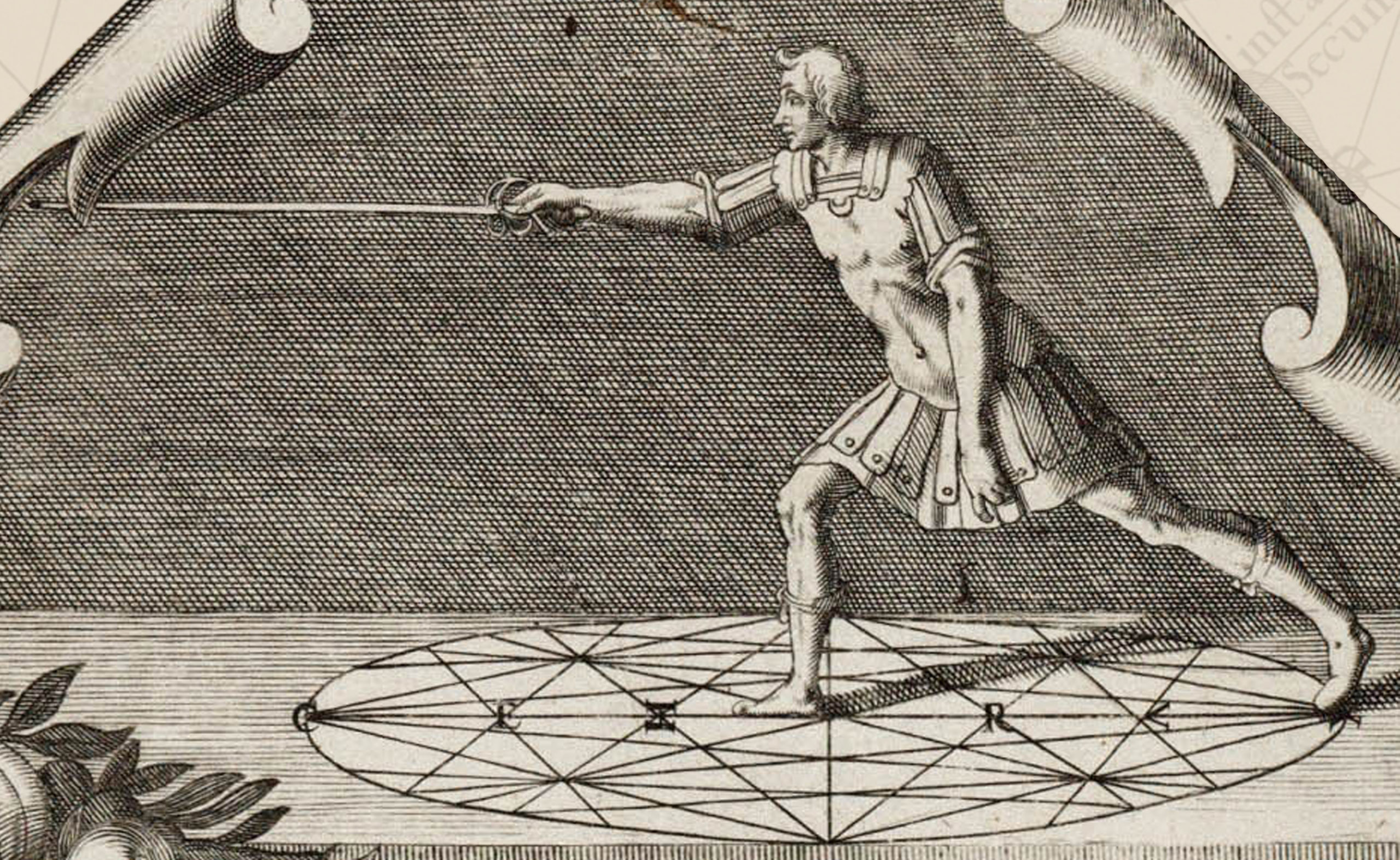
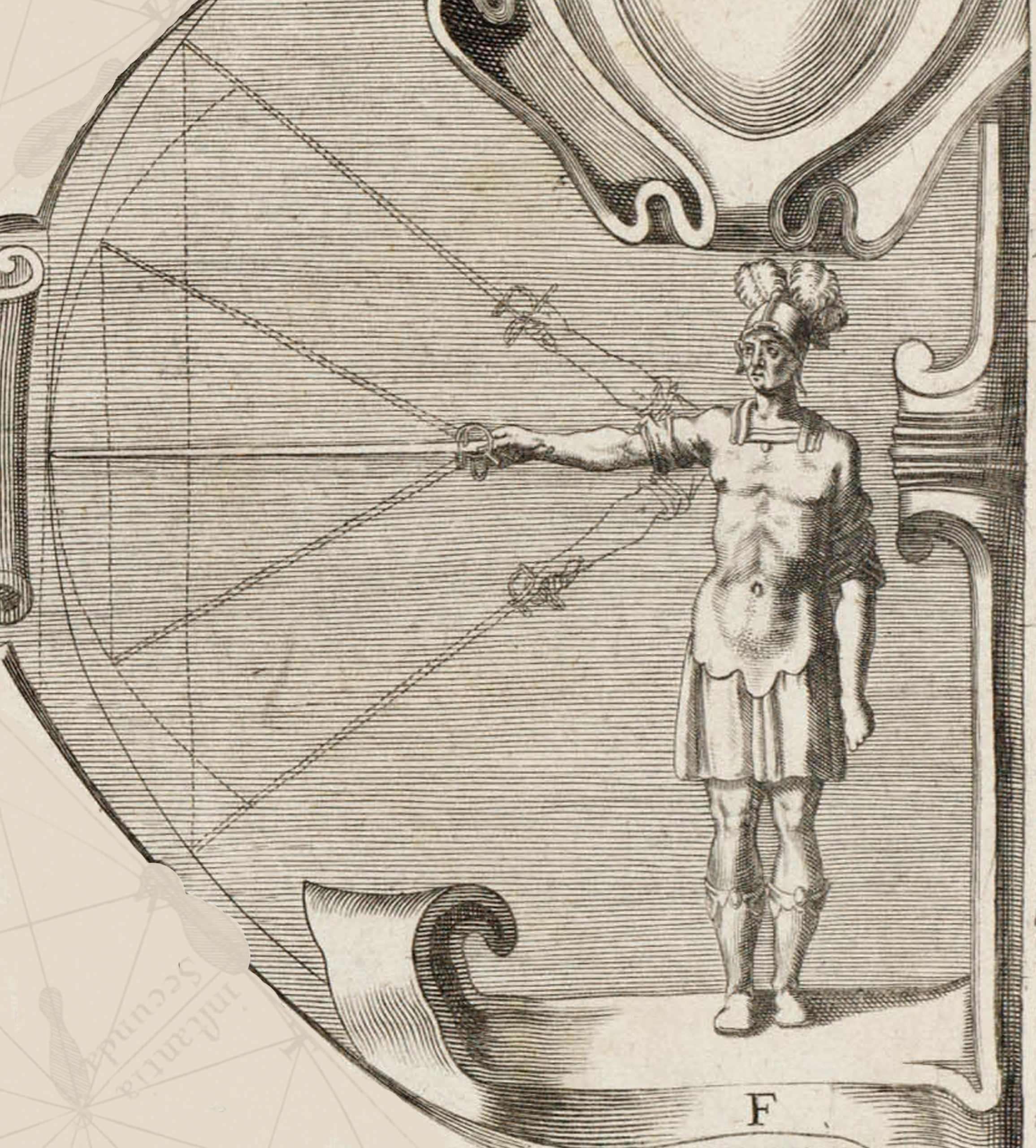
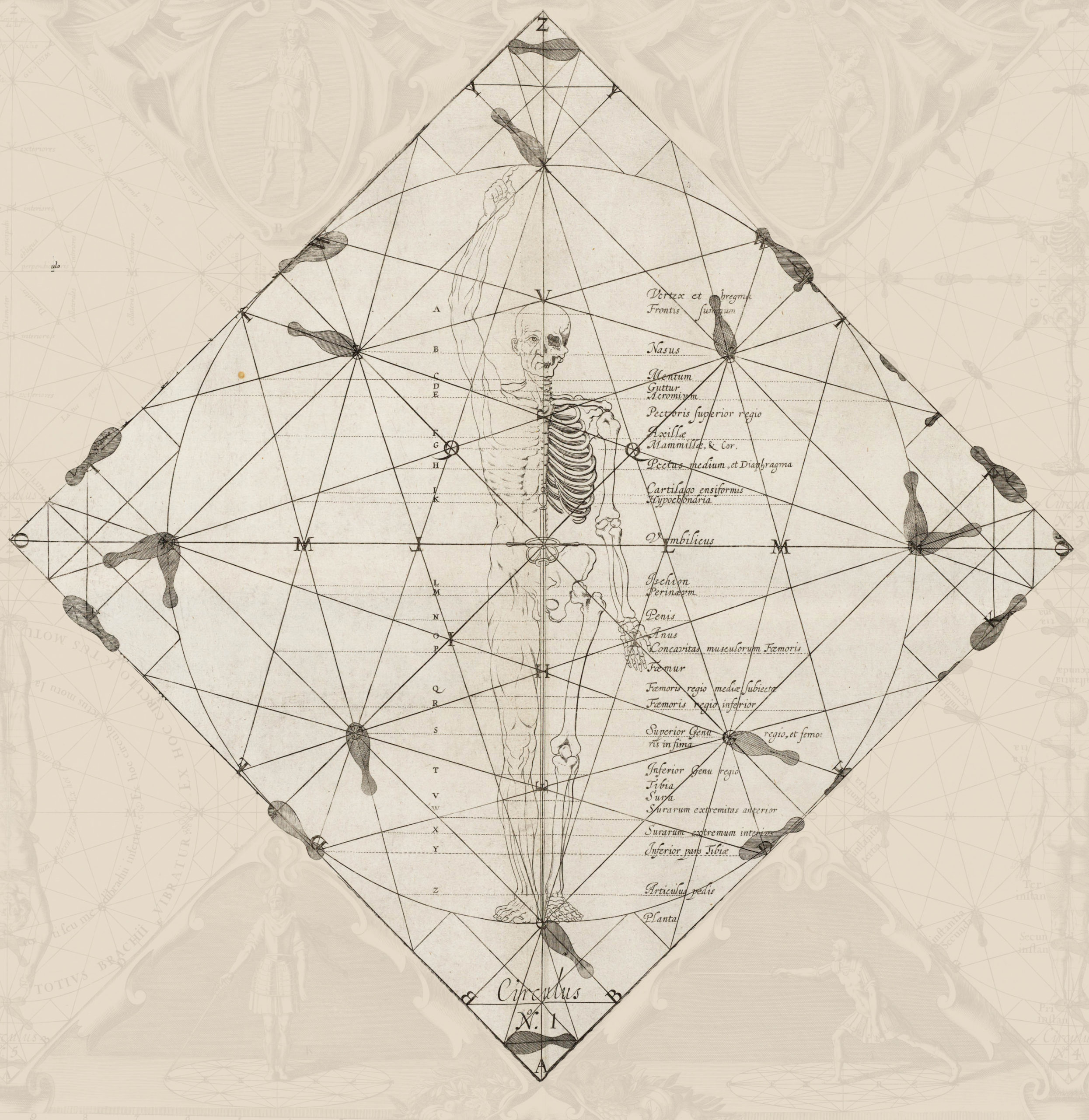
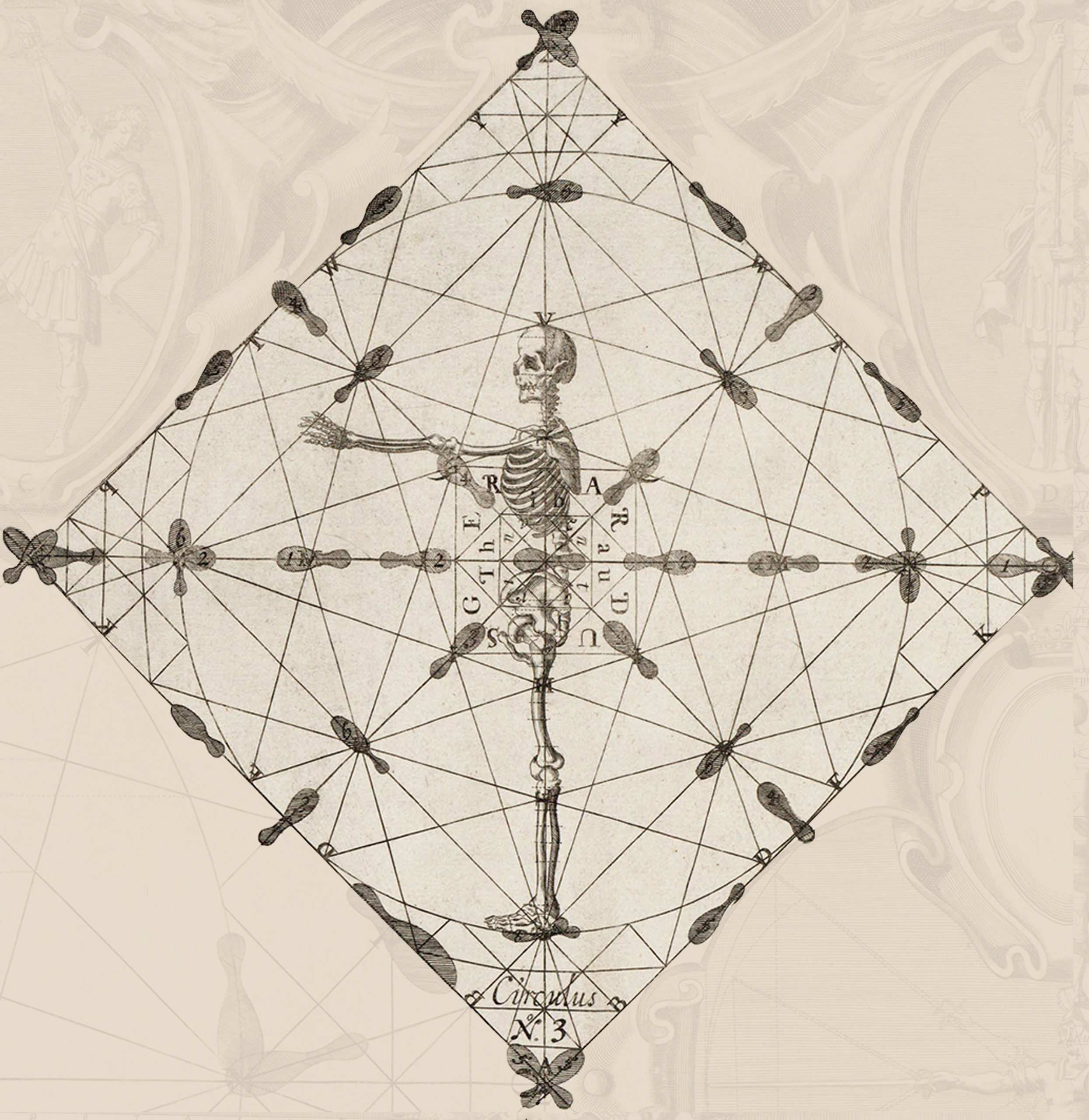
A number of years ago, when I first started researching Gerard Thibault’s ‘Academy of the Sword’ I stumbled across an engraving of the fencing school at the University of Leiden. It showed a number of figures engaging in various martial and acrobatic pursuits and, in the center of the floor was a diagram which, with its circle and collection of lines bore a striking resemblance to Thibault’s ‘mysterious circle.’ Was it possible that this engraving showed Thibault’s fencing school at the University of Leiden? Cursory examination certainly seemed to point in that direction. A deeper look and a bit more information, however, would seem to disprove this theory.

The first strike against this being a representation of Thibault’s school comes from the variety of activities in the image. ‘Academie de l’Espée’ does include the use of the longsword, and the musket and it is clear from the frontispiece of the book that Thibault intended a section on equestrian combat. It should be noted, however, that the sections on alternate weapons are, without exception presented to show the flaws inherent in their use and to support Thibault’s rather vehemently exhorted thesis that the single rapier alone was all that a skilled swordsman needed in any situation against any weapon. Given these views, it seems rather unlikely that a representation of Thibault’s school would have included activities which the he would have considered to be of questionable martial virtue.
The more solid blow, however, arrives when with further information regarding the provenance of the Leiden engraving. According to the library at the University of Leiden, the engraving dates from 1610. In 1610, Gerard Thibault was just returning to Antwerp from his time in Spain. His public exhibition of his “new method” in Rotterdam would not occur until 1611 and, so far as we know, he would not set foot in Leiden until the autumn of 1617 (and then only briefly). In fact Thibault didn’t enroll at the University of Leiden until February of 1622, 12 years after the Leiden engraving was made.
It seems far more likely that the engraving was made to show the fencing school of Ludolph Van Ceulen. Van Ceulen arrived in Leiden around 16 years before the engraving was made and, in June of 1594 petitioned the City of Leiden for a license to open a fencing school. This was not his first such establishment. He had operated a similar fencing school in Delft from 1580-1593. After some negotiations regarding the location, he was given license to open his school in the city church provided that he repair any damage that he or his students might do to the building as a result of their exercise. We do not know precisely how long Van Ceulen taught fencing at Leiden, but in 1610 he fell ill and subsequently died on December 31 of the same year. According to various memorial markers, he continued to hold his professorship in Mathematics until his death. As we know that he was teaching fencing at least as late as 1602, it seems likely that he continued to operate the fencing school up until his illness.
None of this information, however, makes the Leiden engraving any less intriguing. If anything, it only increases the mystery. According to Herman de la Fontaine Verwey’s ‘Gerard Thibault and his Academie de l’espée,’ Thibault’s first fencing instruction came from shermmeester Lambert Van Someren, a prominent member of the Dutch free-masters. Is it possible that rather than originating with Thibault, the ‘mysterious circle’ is, in fact Dutch in origin?
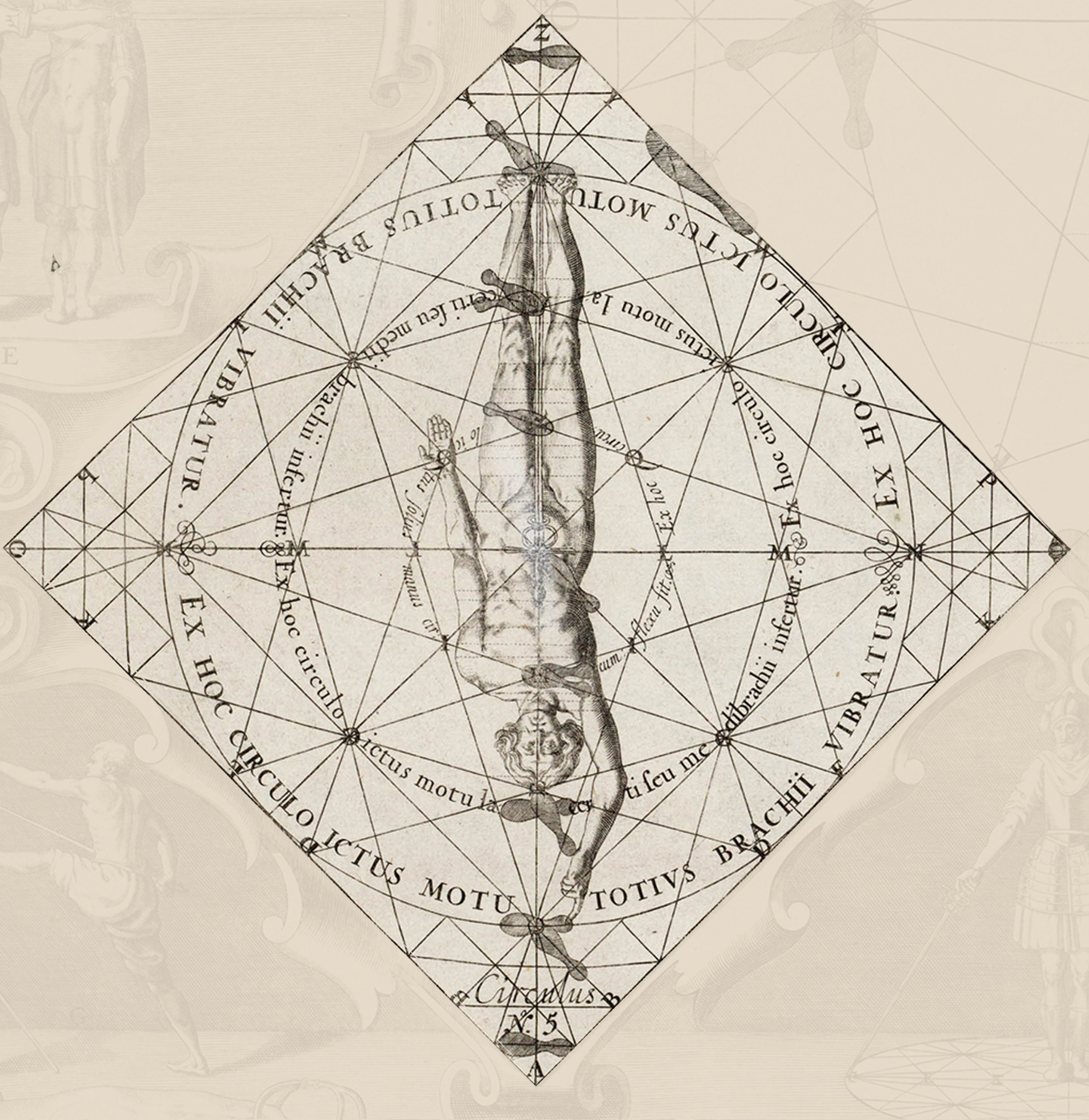
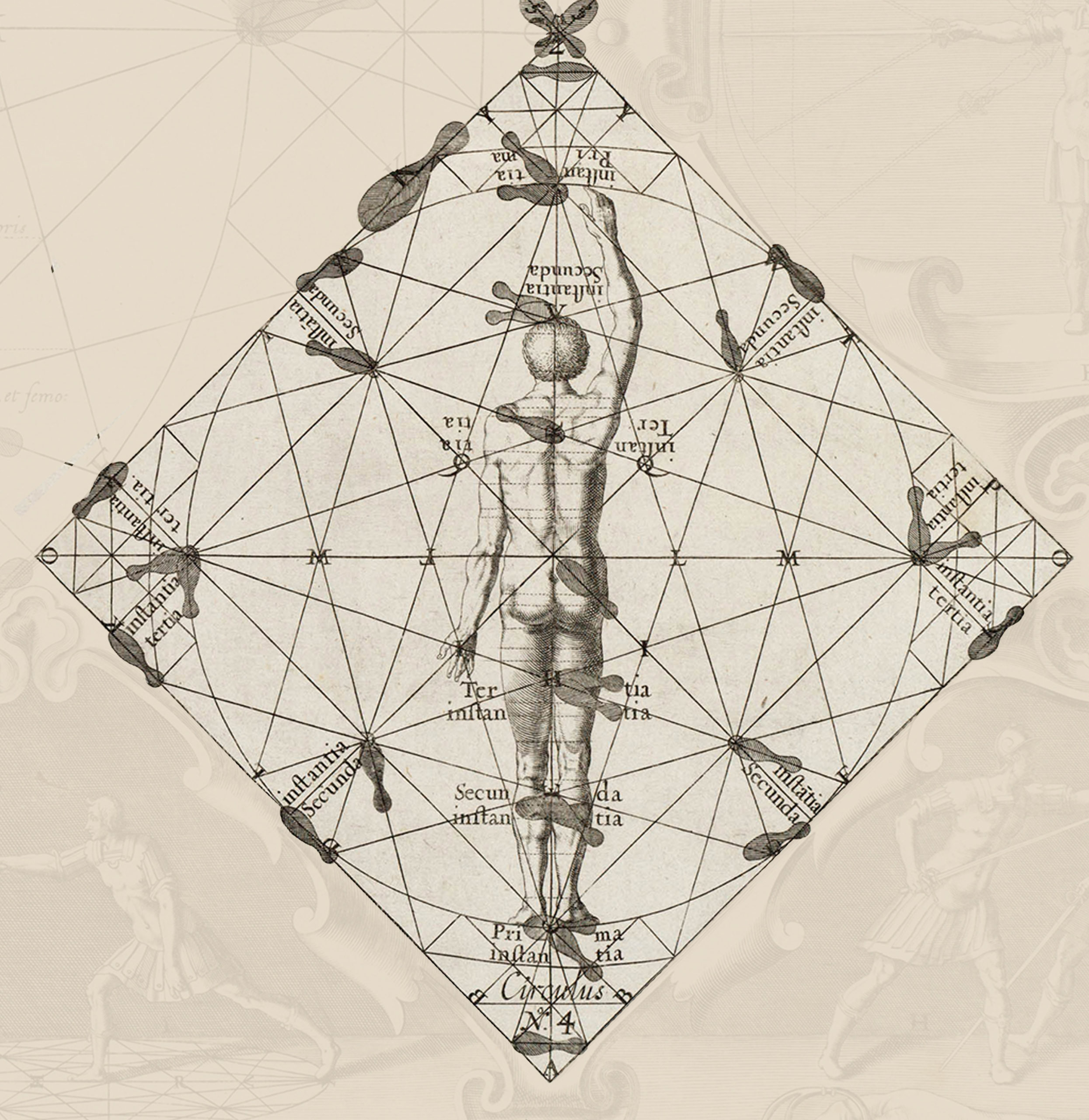
Thibault’s ‘mysterious circle’ and the Leiden diagram certainly bear a striking resemblance to each other but are they, in fact, versions of the same diagram? I decided to reproduce the Leiden diagram on a flat surface, without the rest of the engraving and without the forced perspective. I got my first surprise when I began lining up the points of intersection on the lines.

I had expected the diagram to by symetrical, like Thibault’s. It isn’t. At least it isn’t across the long diameters. Laying the diagram out flat, we see that the what Thibault calls the collateral and transverse lines vary in their angles. Those at the front of the diagram (bottom) intersect with the long diameters and the inscribed square, while those at the rear of the diagram (top) intersect with the long diameters and the circumference (see diagram below).
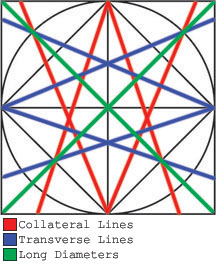
There are any number of reasons why this may have been done. It is possible that this image is used in a different manner than that of Thibault’s. Thibault places his combatants at opposite corners of the diagram at the beginning of his demonstrations. An asymmetry could suggest that steps in one direction are shorter than steps in the other. This seems unlikely, however, since the asymmetry on the Leiden diagram occurs across the horizontal diameter rather than reflecting across one of the long diameters. Given equality of proportion, a step forward and to the left should have the same length for both combatants. The way the Leiden diagram is drawn, this would not be the case.
Likewise, it is possible that the diagram was simply misinterpreted by the engraver. There are several places in the diagram where careful examination shows that the artist altered lines partway down the walls, for example, to correct their angles. These corrections, however, do not show the kind of regularity that we find in the floor diagram. Rather, I believe that the artist altered the diagram slightly to enhance the sense of perspective. A truly symmetrical diagram would have had a tendency to ‘lift’ off of the floor slightly at the back edge. The slight alteration makes the angles at the front of the diagram look much larger than those at the back. From the original diagram, then, we are left with two possible alternate diagrams:
The first, based on the front side of the diagram, has the collateral and transverse lines intersecting with the long diameters at inscribed squares.
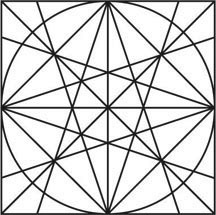
The second, based on the back side of the diagram, has the collateral and transverse lines intersecting with the long diameters at the circumference.
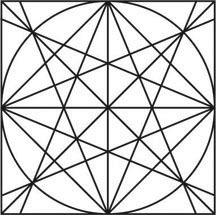
Shown together in perspective, notice how the original version of the Leiden diagram appears to be lying down while the to variants seem to be almost pulling up at the back edge.

It seems likely, that the asymmetry in the Leiden diagram is a function of perspective rather than of usage, but we are still left with the question of how it compares to Thibault’s circle. If the two are variants on the same diagram, it is obvious that the Leiden diagram is a much simpler variant.
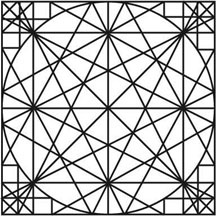
By itself, however, this does not mean they aren’t related. If the artist was willing to make adjustments for perspective, might he not also have simplified the image for clarity? To find out, I overlaid the Leiden diagram with Thibault’s circle. The blue lines in the image represent lines which both diagrams share. The red lines belong to the Leiden diagram and the black lines belong to Thibault’s ‘mysterious circle.’
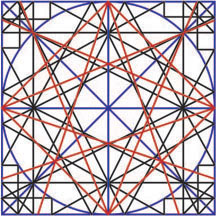
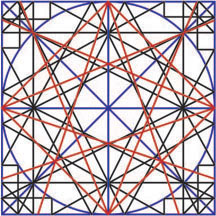
Seen in this way, the points of difference become immediately apparent. The primary difference between the two lies in the orientation of the inscribed square. Thibault’s inscribed square is oriented so that its edges are parallel to the long diameters while the inscribed square in the Leiden diagram has its edges parallel to the short diameters. While this may seem like a minor shift, it effects all of the dependent intersections in the diagram.
Unless we assume that the artist simply did not know what he was looking at, we must conclude that Thibault’s ‘mysterious circle’ was not directly appropriated from an identical Dutch image. One cannot, however fail to contemplate a similarity of origin. It seems likely to me that Thibault learned to fence with the aid of similar diagrams and, finding them pedagogically useful, designed the ‘mysterious circle’ in their image.
Bibliography:
- Greer, John Michael (Translator). Academy of the Sword. Highland Village: Chivalry Bookshelf, 2006
- Thibault, Gerard. Academie de l’Espée. Amsterdam: Elzevier Press, 1630
- Verwey, Herman de la Fontaine. “Gerard Thibault and his Academie de l’espée,” Quarendo. Vol VIII 4/Autumn 1978
- [Oomes 2000] Pi in de bibliotheek: catalogus bij een tentoonstelling over Ludolph van Ceulen en de berekening van het getal pi, in de Leidse Universiteitsbibliotheek, 4-18 juli 2000. Leiden: Universiteitsbibliotheek, 2000.
- [Oomes 2000a] “Het grafschrift van Ludolph van Ceulen”. Nieuw Archief voor Wiskunde 2, 156-161. 2000.